[통계 스터디] 8. 가설 검증 - 불확실성, 오차, 검증력, 일방향/양방향 검증

가설 검증의 논리

: 가설검증이란 모집단 모수에 대한 가설을 평가하기 위해 표본 데이터를 이용하는 표준화된 통계적 절차이다.

1. 알려지지 않은 모집단에 대한 가설을 설정한다.

영가설(귀무가설) H0과 대립가설(대안적 가설) H1, 상반된 2개의 가설을 기술한다.
두 가설 모두 모집단 모수치에 대한 관점에서 기술된다.
- 귀무가설(영가설) H0: 독립변인(처치/자극)이 모집단에 대해 효과를 갖지 못함을 예측.
(변화가 없다/효과가 없다/차이가 없다/관계가 없다)
- 대립가설(대안적 가설) H1: 일반적 모집단에 대해 독립변인이 종속변인에 대해 효과를 갖고 있음을 예측.
(변화가 있다/효과가 있다/차이가 있다/관계가 있다)

2. 유의수준을 통해 의사결정을 위한 영역 즉, 기각역을 설정하라.

실제로 표본을 추출하기 전에, 표본의 특성을 예측하기 위해 가설을 이용한다.

잠재적인 표본집단은 H0이 참일 때 나오기 쉬운 것인지, 나오기 어려운 것인지 두영역으로 나눌 수 있다.

저 발생 가능성이 희박한 확률이 바로 유의수준(ɑ값)이다.
유의수준(ɑ값)이란 H0이 참인지 여부를 판단하기 위해 설정한 확률값이다.
극단 값의 영역에 5%를 설정하여 표본평균의 95%를 설정하는 것이 일반적이다.

ɑ=.05의 기각영역 (나오기 어려운 값들)

기각역은 극단적인 표본값들로 구성되어 있으며, 기각역에 대한 경계는 알파수준에 의해 결정된다.
기각역 내의 값들은 H0이 참일 경우 발생 가능성이 매우 낮은 값이며, 그럼에도 불구하고 표본 데이터가 기각역에 포함되면 H0은 기각된다. 즉, 처치 효과가 없을 경우 발생 자체가 불가능한 표본값으로서, 처치가 효과가 있다는 명백한 증거를 제시하는 표본값인 것이다.

3. 모집단에서 무작위 표본을 추출하여 표본의 검증 통계치를 계산한다.

표본의 원자료는 적절한 통계치로 요약된다. 가설을 표본평균과 같은 통계치, 즉 데이터와 비교하여 가설을 검증한다.
비교는 Z점수를 계산하여 모집단 평균에 대한 표본평균의 상대적 위치를 파악함으로써 이루어진다. (Z검증)

4. 추출한 표본 데이터를 가설의 형태로 진술된 예측과 비교하여 기각 여부를 결정한다.

H0 기각: 계산된 z값이 기각역 안에 포함될 때 -> 처치가 표본 내 개체들에 효과를 냈다고 볼 수 있다.
H0 기각하지 못함: 계산된 z값이 기각역 안에 포함되지 않을 때 -> 처치가 표본 내 개체들에 효과를 내지 못했다고 볼 수 있다.

검정통계량 Z점수

Z점수가 3.00이라는 것은 표본과 가성사이의 획득된 차이가 우연에 의해 기대될 수 있는 것보다 3배 크다는 의미.
유의수준 0.05 혹은 0.01은 적어도 2~3배 큰값을 통해 기각영역을 만족시킬 것을 요구하는 것이다. (더 어려운 것)

오류와 유의수준

- 제1종오류: 실제로 참인 귀무가설을 기각하는 오류. 처치 효과가 없는데, 있다고 결론 내리는 경우. 가설검증이 최소화하고자 하는 타겟. 유의수준은 그 검증이 제1종오류로 귀결될 확률이자, 참인 귀무가설에서 기각영역에서 표본의 데이터를 획득할 확률. 즉 제1종오류의 확률 = 유의수준α
- 제2종오류: 실제로 거짓인 귀무가설을 기각하지 못한 오류. 실제 처치 효과를 탐지하는 데 실패한 것. 처치는 표본에 영향을 줬지만, 효과의 크기는 표본평균을 기각영역 안으로 이동시킬 만큼 충분히 크지 않았다는 의미. 기능적인 값으로서, 단일한 확률값으로 결정하는 것이 불가능해 β로 표현됨.

일반적으로 유의수준 .05를 채택하며(.05, .01, .001), 낮은 유의수준일 수록 제1종오류 발생 가능성은 낮아지지만 그만큼 큰 증거가 요구되는 것. 기각역 내의 표본평균값은 그 확률값 p가 유의수준α보다 작다. 즉, p<α일 때 귀무가설 기각.

Z검증의 가정

1. 무작위 표집 (표본의 모집단에 대한 대표성)
2. 독립적 관찰 (관찰 값 간에 예측적 관계가 없어야 함)
3. 일정한 표준편차 값 (처치의 효과는 평균을 변화시키지만 표준편차에는 변화를 주지 않기 때문!)
4. 정규표집분포 (반드시 표본평균의 분포가 정상분포여야 함)

효과의 크기(effect size)와 검증력 측정

코헨의 d(Cohen's d) = 평균차이 / 표준편차 : 가장 단순하고 직접적인 효과 크기 측정 방법. Z점수의 표준화 방식과 동일. 기술통계. 주로 t분포에 사용되며, 값이 클수록 효과가 큰 것.

이외에도 다양한 효과 크기가 있다.

통계적 검증력: 검증이 그릇된 영가설을 옳게 기각할 확률. 처치효과가 작다면 영가설을 기각하기 쉽지 않을 것이며, 검증력도 낮다고 할 수 있다.

보통 왼쪽 분포 그래프를 그리면서 검정을 진행하는데, 만약 처치 후 집단이 오른쪽 분포처럼 변했을 경우(10점의 효과가 있을 경우)
그 분포가 기존 왼쪽 분포 그래프의 기각역에 거의 100퍼센트가 포함되는 것을 볼 수 있다.
이때, 검증력이 100%라고 해석할 수 있다는 뜻인듯하다.

일방향 가설검증과 양방향 가설검증

방향적 검증
예로, ' H0 음식 소비는 늘지 않을 것이다. vs. H1 음식 소비는 늘 것이다. '와 같은 일방향 가설검증에서 기각영역은 아래와 같다. 기각역의 임계값은 한쪽 꼬리에 할당된 유의수준에 따르며 꼬리 방향은 가설에서 검증하고자 하는 차이의 방향에 따른다. 일방향 검증은 더 민감해 비교적 작은 처치효과도 유의미할 수 있음.

(일방향 가설검증) 크다/안크다 검증으로 기각역은 + 꼬리에 위치

한편, 양방향 검증에서 기각역의 임계값은 꼬리 양쪽에 절반씩 할당된 유의수준에 따른다. 처치 효과가 있다/없다와 같은 매우 큰 차이에 주목할 때 유용한 방식으로, 방향적 기대가 없거나 2개의 상충되는 가설이 있는 경우에 사용한다. 귀무가설을 기각하기 위해 일방향 검증보다 더 강력한 증거를 요구한다.

(양방향 가설검증) 처치효과가 있다/없다 검증으로 기각역은 +, - 양쪽 꼬리에 위치&nbsp;

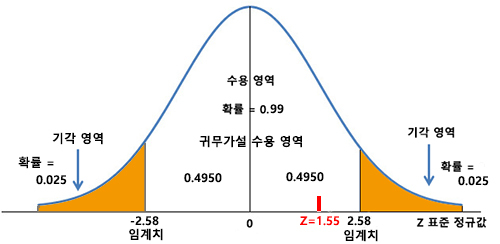
즉, 같은 데이터에 대해서 양방향 검증에서는 기각되지 못하고, 일방향 검증에서는 기각되는 경우가 있을 수 있다! 그렇다고 양방향에서 못얻었다고 단방향을 시도해서는 안된다!

가설검증의 일반적 요소 5가지

1. 가설화된 모집단 모수치
2. 표본 통계치 (표본평균)
3. 오차의 추정 (표준오차): 변산성이 클수록 커지고 표본이 많을수록 작아짐.
4. 검증 통계치 (Z점수)
5. 유의수준 α: p<α일 때 귀무가설 기각

뒤 이어서 나올 여러 검증 과정에도 이 다섯가지가 사용된다.

http://www.ssacstat.com/default/cs/cs_05.php?com_board_basic=read_form&com_board_idx=41&topmenu=5&left=5&&com_board_search_code=&com_board_search_value1=&com_board_search_value2=&com_board_page=8&

http://www.ssacstat.com/default/cs/cs_05.php?com_board_basic=read_form&com_board_idx=41&topmenu=5&left=5&&com_board_search_code=&com_board_search_value1=&com_board_search_value2=&com_board_page=8&

https://blog.naver.com/PostView.nhn?blogId=jaysrogers&logNo=222120255577&parentCategoryNo=&categoryNo=108&viewDate=&isShowPopularPosts=true&from=search

효과 크기(effect size)란 무엇인가? p값(p-value)란 무엇인가?

[참고] 사회과학 통계방법론의 핵심 이론 (커뮤니케이션북스)