[통계 스터디] 5. 표준점수 - 표준화된 분포, Z 점수

Z점수(표준점수)란.

: z=(X-µ)/σ (X-µ: 편차점수, zσ: X의 편차, X=µ+zσ)

분포안에서 개별 점수의 위치를 구체화하고, 부호를 통해 개별 점수가 평균보다 큰지 작은지를 파악할 수 있다. Z점수 절대값은 개별 점수와 평균 사이의 거리를 표준편차의 배수로 표현한 것으로 볼 수 있다. 

 

Z점수(표준점수)의 목적

1. 분포 속에서 모든 점수의 정확한 위치를 묘사하고 구체화하는 것

2. 다른 분포와 비교될 수 있는 표준화된 분포 형성

 

Z분포의 속성

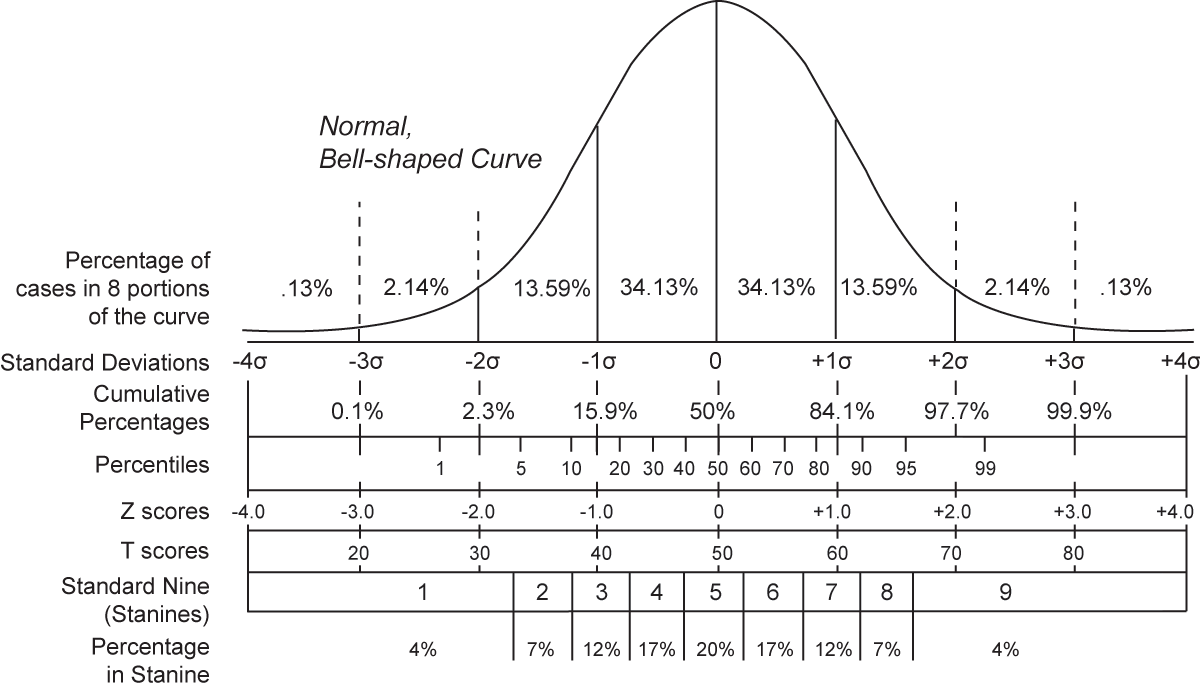
- 원점수 분포와의 형태 동일

- 평균 항상 0 (Z점수 양의 값은 평균보다 위, 음의 값은 평균보다 아래)

- 표준편차 항상 1

 

 

 

 

Z분포의 활용

- Z점수를 이용해 새로운 평균과 표준편차를 갖는 분포로 변환 가능

  (예. 심리학, 교육학 분야에서 검사 결과 점수를 특정 평균과 표준편차를 갖는 분포로 전환하는 경우 빈번)

- 어떤 조작적 행동이 모집단의 개체에 유의한 영향을 미쳤는지 검증하는 데에 사용. 

- 0에 가까운 z점수는 모집단의 평균에 가깝고, 전형적인 케이스임을 의미. +2.00 이상 혹은 -2.00 이하의 z점수는 매우 극단적이며, 분포의 다른 값 대비 두드러지게 다름을 의미.

 

연구에서 조작을 받은 개체가 분포 내에서 극단의 z점수를 갖는 경향이 있다면 그 조작이 효과가 있다고 결론지을 수 있다.

 

[참고] 사회과학 통계방법론의 핵심 이론 (커뮤니케이션북스)