[통계 스터디] 6. 확률 - 확률과 정규분포

확률(p, probability)이란.

서로 다른 결과가 나올 수 있는 상황에서 특정 결과가 나올 비율 → 모든 확률 문제는 비율 문제로 바꿔 말할 수 있다. 

P(A)=(특정 사건이 발생할 수 있는 경우의 수)/(발생 가능한 모든 경우의 수)

모집단과 표본 사이를 어떻게 연결해야 할지를 알려주며, 이는 추론 통계의 기초가 되는 개념이다.

확률은 제한된 범위 0~1에서 움직인다.

 

무작위 표집(Random sample)

확률을 이용해 모집단, 표본의 특성을 유추해 낼 때 표본은 무작위 표집으로 뽑은 무작위 표본이어야한다. 

1. 모집단의 모든 개체는 뽑힐 수 있는 동일한 기회를 가져야 하며,

2. 복원추출 방식으로 모집단은 최초 상태 그대로 유지해야 무작위 표집이라 할 수 있다. 

cf. 단일무선표본, 독립적 무선표본

 

모집단이 빈도분포 그래프로 제시될 때, 그래프의 비율로서 확률을 표현할 수 있다. 

 

확률과 정규분포

각 영역이 차지하고 있는 점수의 백분율을 보여준다.

- 정규분포곡선의 대칭성: 분포의 한쪽면은 동일한 비율로 반대면에 대응

- z점수로 규정되는 분포의 위치: 그림의 비율은 평균과 표준편차 값에 상관없이 어떤 정규분포에도 적용 가능

정규분포표

P(X<?)→P(Z<0.32)로 정규화한 후, 정규분포표에서 확률을 찾는 과정 (출처: https://math100.tistory.com/39)  정규분포의 대칭성을 이용해 여러 비율을 구할 수 있다. 

 

정규분포표 문제 풀기.

: 계산 시에는 분포도를 그려야 실수를 줄일 수 있다

(1) 구체적인 z점수에 해당하는 확률값 찾기

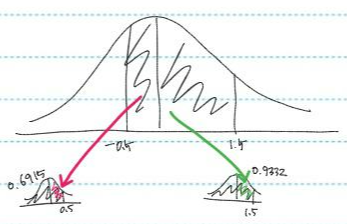
  예: P(-0.50<z<1.5)=P(z<0.5)-0.5+P(z<1.5)-0.5=0.1915+0.4332= 0.6247

예: P(-0.50&amp;lt;z&amp;lt;1.5)=P(z&amp;lt;0.5)-0.5+P(z&amp;lt;1.5)-0.5=0.1915+0.4332= 0.6247

(2) 특정 확률에 해당하는 z점수의 위치 구하기

  (예: 정규분포에서 상위 10%를 분할하는 z점수는? z=1.28)

 

* 아래 삼각 관계에 따라 z점수가 알려지지 않은 상태의 구체적인 변수값 X에 대한 (1), (2) 문제 풀기도 가능하다. 일반적으로 문제 출제는 여기서 된다.

삼각관계. X와 확률은 직접 연결이 불가능하다!

 

추론통계 엿보기

왼쪽 도식의 조사연구에서 처치효과를 평가하는 데 이용되는 확률은 오른쪽을 통해 얻을 수 있다. 낮은 확률인 영역을 보이는 z값은 처치 전의 원래모집단에서 거의 얻을 수 없는 값으로서, 처치효과의 증거로 간주된다. 

 

[참고] 사회과학 통계방법론의 핵심 이론 (커뮤니케이션북스)