ANOVA: 둘 이상의 표본평균을 비교할 수 있지만 13장의 내용은 여전히 한 가지 특정 유형의 연구조사(단일 요인설계)로 한정되어 있음.
단일 요인설계는 단 한가지의 독립변인만을 고려한 ‘독립측정 방식’.
- 단일요인 독립측정: 비교할 각각의 처치 조건을 위해 독립된 표본을 이용
- 단일요인 반복측정: 서로 다른 모든 처치 조건에서 동일한 표본을 이용
단일요인, 독립측정에 더 나아가서 아래와 같이 ANOVA를 이용한 보다 복잡한 연구 상황을 살펴보자.
1. 반복측정 ANOVA: 모든 처치조건에서 동일한 참가자를 이용하는 반복측정 조사연구를 활용해 다른 처치조건 비교 가능.
2. 2요인 ANOVA: 어떻게 행위가 다른 2개의 변인에 영향을 받는지의 연구문제에 이용.
1. 반복측정 ANOVA
모든 처치 조건에서 동일한 참가자를 이용하는 2개 혹은 그 이상의 처치조건을 비교하는 연구에서 얻은 평균 차이를 평가하는 데 사용
단일 요인 반복측정: 다른 모든 처치 조건에서 동일한 표본을 이용. 서로 다른 조건들로 독립변인을 조작하지 않는 비실험적 연구에서 이용.
가설: $$H_0=\mu_1=\mu_2=\mu_3=…$$
검증통계치: F비율 (처치 간 변량(차이))/(우연 혹은 오차로 인한 변량(차이), 잔차변량, 오차변량)= (처치효과+우연or오차(개인적차이를 배제한)) / 우연or오차(개인적차이를 배제한)
- 처치 간 변량의 원인: 처치효과, 우연or오차
- 처치 내 변량의 원인: 개인적 차이, 우연or오차
-> 개인적 차이를 처치 간 변량과 F비율의 오차항 둘 다 변산성의 원인으로 갖는 독립측정 ANOVA와 다르다. 2단계의 차이
$$F=\frac{MS_(처치 간)}{MS_오차}$$ (처치효과가 없으면 1, 영가설 기각 실패)
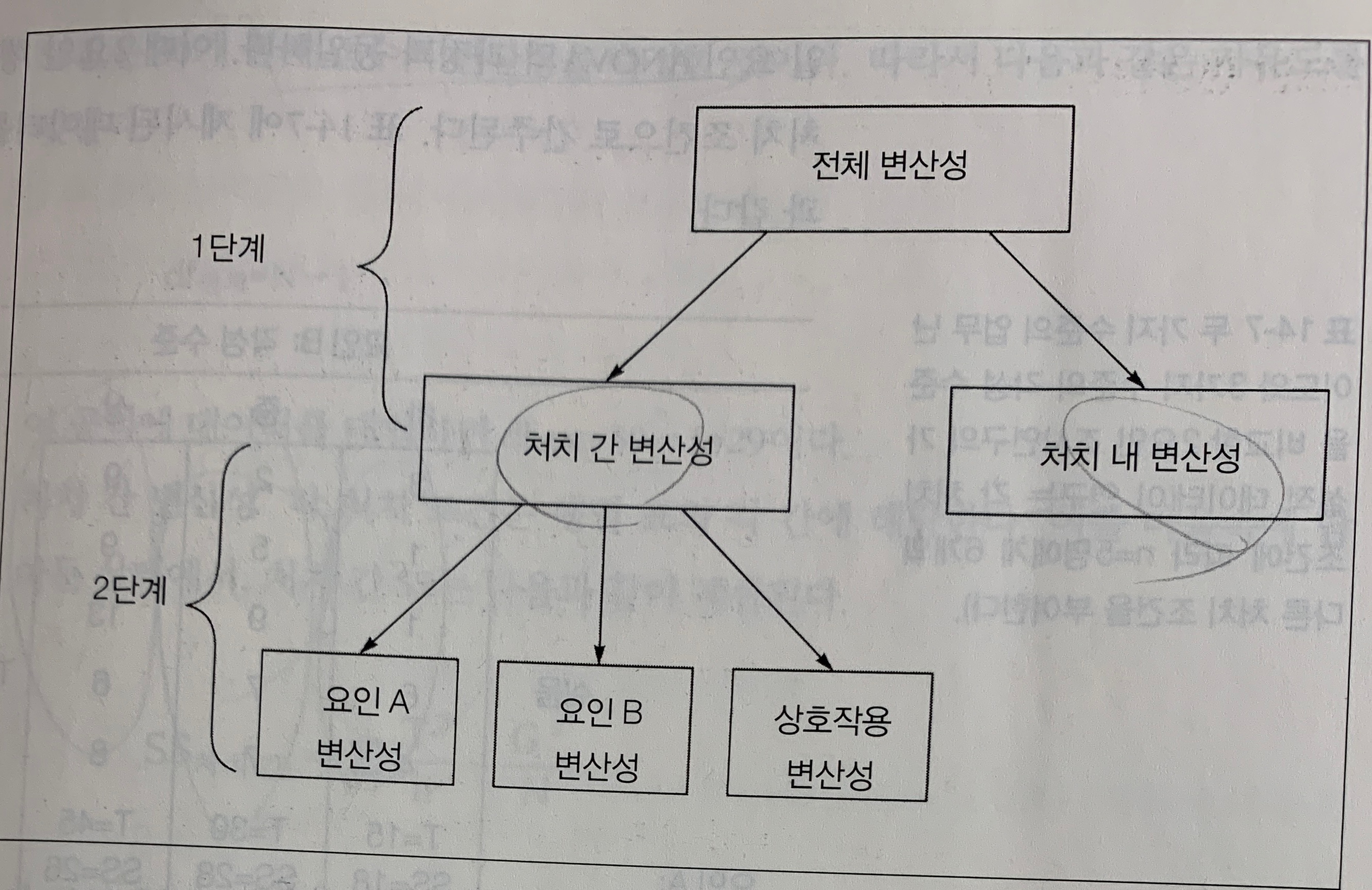
F비율 분모를 얻는 2단계
1단계. 전체 변산성을 처치 간, 처치 내 두 구성요소로 나눈다.
: 모든 처치 조건에서 동일한 참가자를 이용하므로 처치 간 차이에 개인차는 발생하지 않으며(처치 내엔 有), 개인차는 F비율의 분자인 처치 간 변량으로 인해 자동 제거됨
2단계. 피험자 간 변산성을 계산한 후 SS와 df값을 해당 처치 내 값에서 뺀다.
잔차는 개인차를 제외한 오차의 측정이며, F비율의 분모에 해당된다.
SS오차=SS처치내-SS피험자간
$$F=\frac{\frac{SS_{처치간}}{df_{처치간}}}{\frac{SS_{오차}}{df_{오차}}}$$
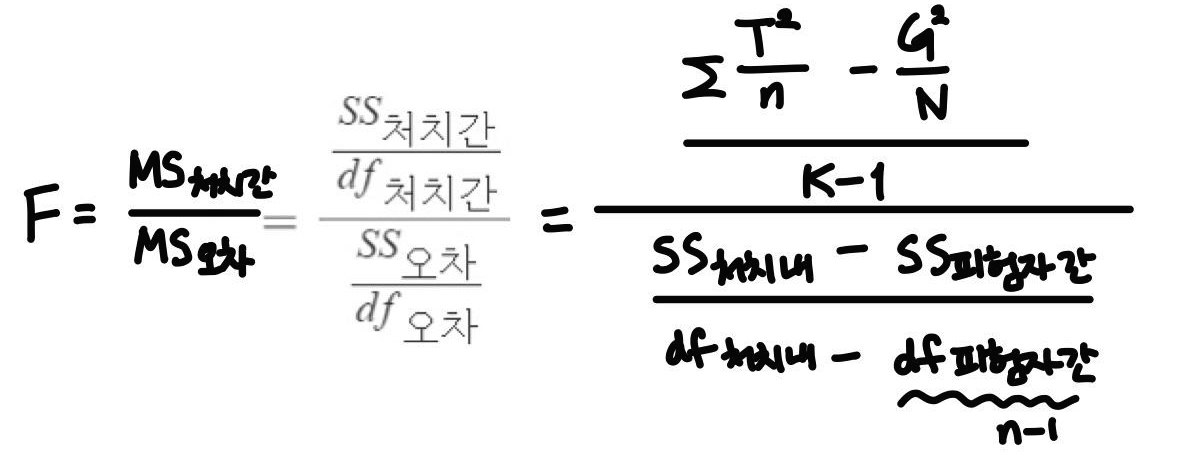

2. 2요인 ANOVA
한 요인의 수준과 다른 한 요인의 수준을 교차시켜 나열한 행렬표로 도표화하며, 각 셀은 두 요인의 특정 조합에 해당.
두 요인은 요인A와 요인B로 정의한다.
변량분석의 목적은 실험적 행렬 표 안의 셀들 혹은 처치 조건들 사이에 어떤 유의미한 평균 차이가 있는지를 결정한다.
주효과: 하나의 요인 수준 사이에 존재하는 평균 차이. 1요인과 2요인 간의 평균 차이.
- A효과: 차이 효과가 요인A의 다른 수준에 의해 발생한다.
- B효과: 차이 효과가 요인B의 다른 수준에 의해 발생한다.
상호작용효과: 두 요인을 조합함으로써 얻는 평균 차이. 개별적 처치 조건 사이의 평균 차이가 요인들의 전체 주효과로 예측될 수 있는 것과 서로 다를 때 발생한다.
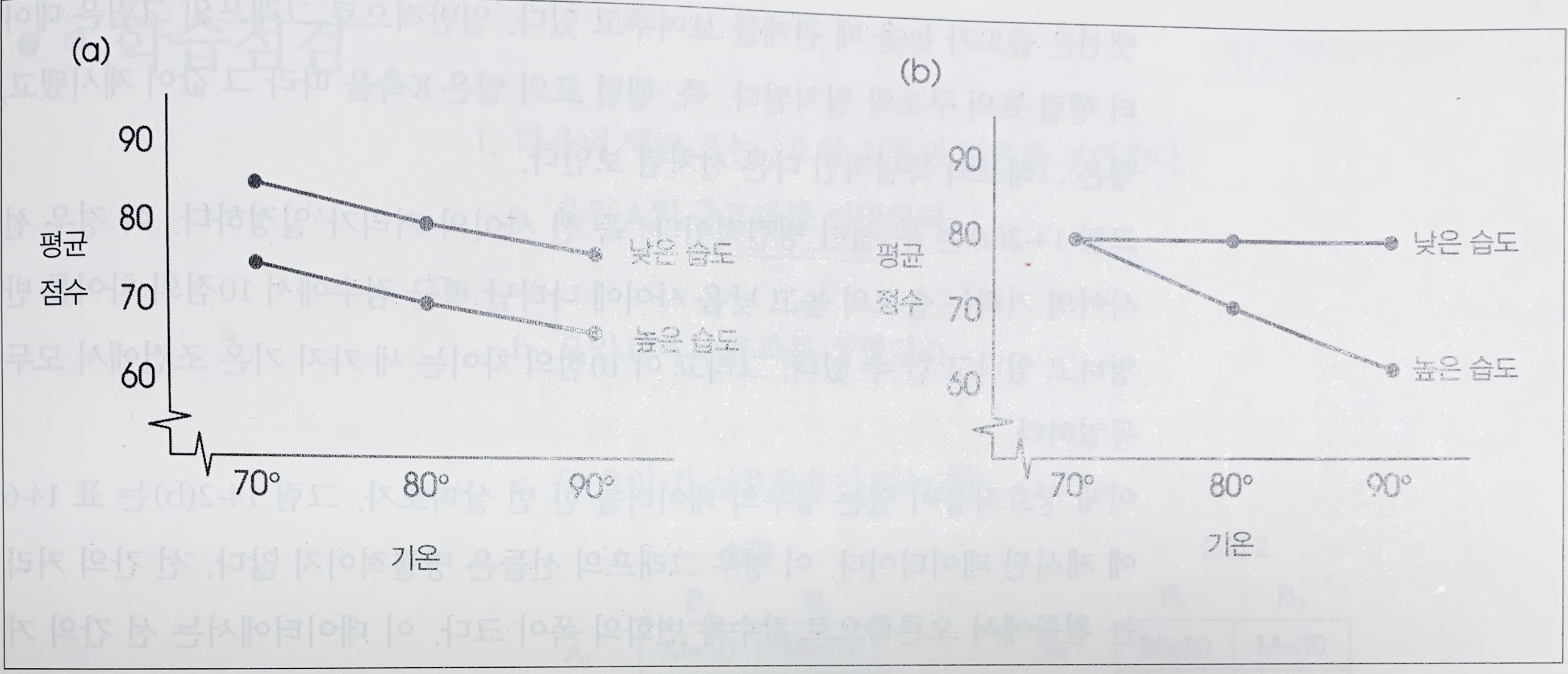
- A*B 상호작용: A와 B의 특정 조합에 의해 발생하는 차이. 상효작용은 한 요인이 다른 요인의 상이한 수준에 따라 영향을 받을 때(종속적일 때) 발생. $$ F=\frac{주효과로 설명되지 않은 변량(평균차이)}{MS_처치 내}$$
처치평균 그래프를 통해 비병렬적 선을 확인하는 것은 상호작용을 인식하는 가장 쉬운 방법!
영가설: 요인A와 요인B 사이에 상호작용이 없다(독립적). 처치 조건 사이의 모든 평균 차이는 두 요인의 주효과에 의해 예측, 설명될 수 있다.
검증통계치: 3개의 F비율 (A요인, B요인, A*B 상호작용. 각 F비율은 동일한 기본 구조 가짐) $$ F=\frac{MS_처치효과(A 또는B또는A*B}{MS_처치내}$$
[참고: 사회과학 통계방법론의 핵심이론]
'공부 > 통계·ML' 카테고리의 다른 글
| Data granularity와 Aggregation (0) | 2022.08.10 |
|---|---|
| [통계 스터디] 16. 카이스퀘어: 적합도와 독립성검증 (0) | 2022.06.03 |
| [통계 스터디] 13. 일원 변량분석(ANOVA) - 변량분석, F분포, 사후검사 (0) | 2022.06.01 |
| [통계 스터디] 12. 추정 - 점추정, 구간추정, 신뢰구간 (0) | 2022.04.15 |
| [통계스터디] 11. 대응/상관표본 t검증 (0) | 2022.04.08 |